The Monty Hall Problem

Luke brought up the Monty Hall Problem the other day. The structure is simple and my intuition led me astray.

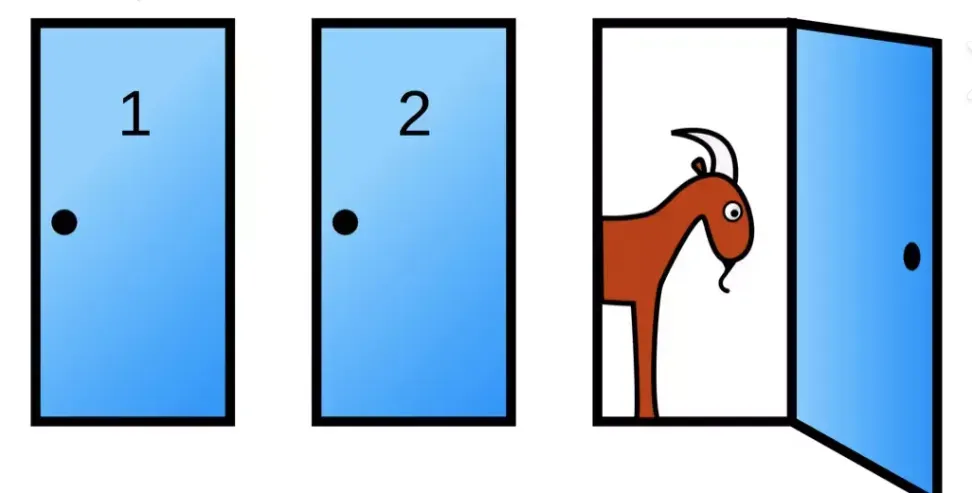
Imagine you are on a game show. You are presented with three doors. Behind one of them is a new car, while the other two contain goats. You want the car. You pick one door at random. The host opens one of the two doors you didn’t pick - and always reveals one of the goats. Before the car is revealed, you are now given a choice; do you want to switch your choice to the other door?

My gut? It doesn’t matter. You have a 50/50 chance of picking the car now and so it is no better than a coin flip. Switch, or don’t switch, it won’t make a difference. I didn’t want to get “fooled” into thinking the door-with-goat-behind-it revelation changed things materially.

The answer? It really matters and you always want to switch doors. The whole Wikipedia article above is worth reading, but since I’m more of a simulation than mathematical proof person, we wrote a simple C# program.

Over the past couple of days, we’ve run well north of 10 billion simulations. The answer is unequivocally clear. Always switch. The key insight is that you have gained new information because the host deterministically opened one of the two doors containing a goat.

Here is a recent run of 100,000,000 simulations, randomly picking whether to switch doors or not each time. You win 2/3rds of the time you switch, and only 1/3rd when you don’t. That’s a real boost in winning!

Monty Hall Simulator 

Running 100,000,000. 

We played 100,000,000 games. 

The player switched doors in 49,997,950 games, 50.00% of the time. 

The player won 66.66% when switching and 33.34% when they didn't switch.

We weren’t alone in getting fooled. The vast majority of people, even people who should know better, believe it doesn’t matter at first.

If you are interested in trying out for yourself, here is the code we wrote. It’s rough, but gets the job done!